通过一个简单的二叉树例子,捋一捋思考的思路
比如需要对下列数组进行排序
int[] arr = {17, 12, 19, 10, 15, 18, 25, 8, 11, 13, 16, 22};
这里可以根据数组里的元素创建一个二叉树,要求就是父节点的值大于左子树节点的值,不大于右子树节点的值;当然父节点的值不小于左子树节点的值,小于右子树节点的值也行,最后再按中序遍历进行输出,也就是左中右,那么就能保证从小到大排序输出
具体二叉树如下
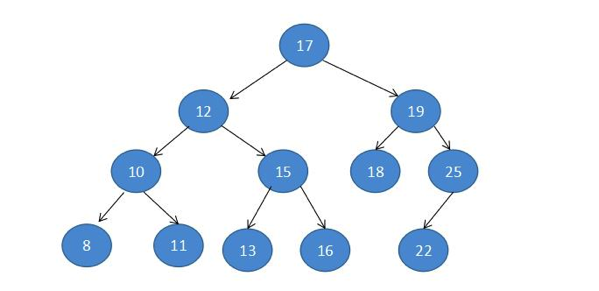
首先添加一个Node类,二叉树由很多个Node组成,Node类里定义三个成员变量,一个是值,这里是整型数字,还有分别指向左子树和右子树Node的引用,同时添加构造方法
package Love;
public class Node {
private int data;
private Node left;
private Node right;
public Node() {
}
public Node(int data) {
this.data = data;
}
}
然后添加一个BinaryTree类,一个根节点即可,构造方法不写也可以,不用传参
package Love;
public class BinaryTree {
private Node root;
public BinaryTree() {
}
}
考虑到需要将数组里所有整型元素添加到一个一个Node里,首先得添加Node,BinaryTree类里得实现addNode方法,先考虑第一个Node的情况,本来二叉树为空,root为null,在创建第一个Node保存data为17的时候,直接用root来引用,因此第一个分支,将data传进去创建一个Node,根root引用即可
package Love;
public class BinaryTree {
private Node root;
public BinaryTree() {
}
public void addNode(int data) {
if (root == null) {
root = new Node(data);
}
}
}
然后再来考虑root不为null的时候,比如这时根节点已经非null,那么创建第二个Node的时候,需要知道对应的data和17的大小关系,如果比17小,就放到left子树节点里,如果大于或者等于17,就放到right子树节点里,这段逻辑可以在Node类里添加一个add方法来实现,而在BinaryTree类里addNode方法只需要调用父节点的add方法,传入父节点的data值供add方法来判断
具体add的实现逻辑:
如果新来的data比root节点的data小,那么就需要在root的左边创建这个Node,如果此时left子树节点为空,那么就直接new一个left子树Node,值为data;如果此时left子树节点非空,那么就递归,root.left再次调用add方法,进行逻辑判断最终创建Node
如果新来的data比root节点的data不小于,那么就需要在root的右边创建这个Node,如果此时right子树节点为空,那么就直接new一个right子树Node,值为data;如果此时right子树节点非空,那么就递归,root.right再次调用add方法,进行逻辑判断最终创建Node
package Love;
public class Node {
private int data;
private Node left;
private Node right;
public Node() {
}
public Node(int data) {
this.data = data;
}
public void add(int data) {
if (this.data > data) {
if (this.left == null) {
this.left = new Node(data);
} else {
this.left.add(data);
}
} else {
if (this.right == null) {
this.right = new Node(data);
} else {
this.right.add(data);
}
}
}
}
这里完事之后,就再回到BinaryTree类里,完成addNode方法里的else,如果root非空,就需要添加字树节点,具体调用add方法来完成
package Love;
public class BinaryTree {
private Node root;
public BinaryTree() {
}
public void addNode(int data) {
if (root == null) {
root = new Node(data);
} else {
root.add(data);
}
}
}
到这里整个二叉树就创建完了,测试一下是否出现问题,main里调用一下二叉树的创建,编译运行不出错即可
package Love;
/**
* Hello world!
*/
public class App {
public static void main(String[] args) {
int[] arr = {17, 12, 19, 10, 15, 18, 25, 8, 11, 13, 16, 22};
BinaryTree bt = new BinaryTree();
for (int a : arr) {
bt.addNode(a);
}
}
}
再来考虑输出,BinaryTree类里添加一个printNode方法打印输出,如果root为null,也就是二叉树里啥都没有,那就不打印不管了,非null同样就直接调用Node的print方法
package Love;
public class BinaryTree {
private Node root;
public BinaryTree() {
}
public void addNode(int data) {
if (root == null) {
root = new Node(data);
} else {
root.add(data);
}
}
public void printNode() {
if (root != null) {
root.print();
}
}
}
再来实现Node类里的print方法,这里输出的方法是中序遍历,也就是先左子树,然后父节点,最后右子树
先左子树,如果为null,不管了;如果非null,说明左子树节点已经有了,但是有可能左子树节点并不是叶子节点,还有子树,因此这里直接递归,通过this.left作为父节点调用print方法进行递归
然后父节点,上面左边一堆输出完了之后,就直接输出当前this.data
最后右子树,如果为null,不管了;如果非null,说明右子树节点已经有了,但是有可能右子树节点并不是叶子节点,还有子树,因此这里直接递归,通过this.right为父节点调用print方法进行递归
这里的递归,比如图中;先找到17,调用print,发现有左子树12,调用print,发现有左子树10,调用print,发现有左子树8,调用print,这部分就是一直递归,条件就是this.left != null,而8是叶子节点,是此时的this,this.left = null,因此就打印8,this.right = null,退回到10作为this,左子树8这边输出完了,输出10,接着this.right != null,递归右边,11变成了this,当然这里11也是叶子节点,因此只打印一个11,假如此时11还有个左子树和右子树非null,又要将11作为this,先递归left,打印11,再递归right,如此循环
package Love;
public class Node {
private int data;
private Node left;
private Node right;
public Node() {
}
public Node(int data) {
this.data = data;
}
public void add(int data) {
if (this.data > data) {
if (this.left == null) {
this.left = new Node(data);
} else {
this.left.add(data);
}
} else {
if (this.right == null) {
this.right = new Node(data);
} else {
this.right.add(data);
}
}
}
public void print() {
if (this.left != null) {
this.left.print();
}
System.out.print(this.data + " ");
if (this.right != null) {
this.right.print();
}
}
}
最后再在main调用二叉树中序遍历的输出方法
package Love;
/**
* Hello world!
*/
public class App {
public static void main(String[] args) {
int[] arr = {17, 12, 19, 10, 15, 18, 25, 8, 11, 13, 16, 22};
BinaryTree bt = new BinaryTree();
for (int a : arr) {
bt.addNode(a);
}
bt.printNode();
}
}
输出结果正确无误
8 10 11 12 13 15 16 17 18 19 22 25
如果需要三种遍历方式,只需要修改Node类里的输出方法即可
public void preOrderPrint() {
System.out.print(this.data + " ");
if (this.left != null) {
this.left.preOrderPrint();
}
if (this.right != null) {
this.right.preOrderPrint();
}
}
public void inOrderPrint() {
if (this.left != null) {
this.left.inOrderPrint();
}
System.out.print(this.data + " ");
if (this.right != null) {
this.right.inOrderPrint();
}
}
public void postOrderPrint() {
if (this.left != null) {
this.left.preOrderPrint();
}
if (this.right != null) {
this.right.preOrderPrint();
}
System.out.print(this.data + " ");
}
输出结果和二叉树图一致
17 12 10 8 11 15 13 16 19 18 25 22
8 10 11 12 13 15 16 17 18 19 22 25
12 10 8 11 15 13 16 19 18 25 22 17
