Given an array of integers nums sorted in ascending order, find the starting and ending position of a given targetvalue.
Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8 Output: [3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6 Output: [-1,-1]
一个已经排序好的数组,找到给定target所在的起始位置和最后的位置,复杂度logn
看到复杂度logn,肯定又是二分相关的
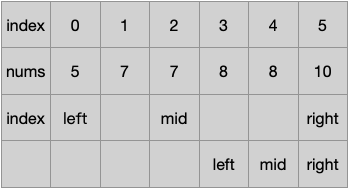
假如中位数nums[middle] < target,如下图,那么target肯定在mid的右边,因此left = middle + 1
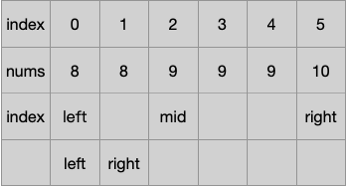
假如中位数nums[middle] > target,如下图,那么target肯定在mid的左边,因此right = middle – 1
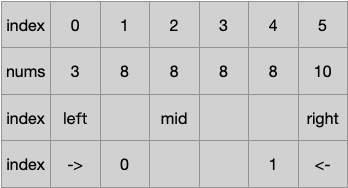
根据上面两种情况的不停缩小区间,最终当nums[middle] == target时,因为无法确认到底有多少个target,因此只需要两边各遍历一次即可,左边从左往右找index,右边从右往左找index
最后假如没找到,返回-1,可以赋个初值
Java源码
package com.lihuia.leetcode;
/**
* Copyright (C), 2018-2019
* FileName: ThirtyFour
* Author: lihui
* Date: 2019-08-15
*/
public class ThirtyFour {
public int[] searchRange(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int[] indexs = new int[]{-1, -1};
if (right == -1 || nums[left] > target || nums[right] < target) {
return indexs;
}
while (left <= right) {
int middle = left + (right - left) / 2;
if (nums[middle] < target) {
//[5,7,7,8,8,10] target = 8 [3,4]
left = middle + 1;
} else if (nums[middle] > target) {
//[8,8,9,9,10] target = 8 [1,2]
right = middle - 1;
} else {
for (int i = left; i <= middle; i++) {
if (nums[i] == target) {
indexs[0] = i;
break;
}
}
for (int i = right; i >= middle; i--) {
if (nums[i] == target) {
indexs[1] = i;
break;
}
}
return indexs;
}
}
return indexs;
}
}
Python山寨一下上面代码即可
class Solution(object):
def searchRange(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
left = 0
right = len(nums) - 1
if (right == -1 or nums[left] > target or nums[right] < target):
return [-1, -1]
while left <= right:
middle = left + (right - left) / 2
if nums[middle] < target:
left = middle + 1
elif nums[middle] > target:
right = middle - 1
else:
while left <= middle:
if nums[left] == target:
break
left += 1
while right >= middle:
if nums[right] == target:
break
right -= 1
return [left, right]
return [-1, -1]
OVER